简单记录一下计算机图形学中需要的光学基础，并以此重新复习一下BRDF光照模型。

物理光学

光学的分类

       光学有两个重要的分支，分别是几何光学和波动光学。

图形学的光学需求

       计算机图形学中使用几何光学，但是几何光学模型仍然过于复杂，因此，计算机图形学中的几何光学模型，相比物理学中的几何光学模型继续做了如下简化：

  1. 物体表面是绝对光滑(smooth)的
  2. 光只可以被发射(emitted)，反射(reflected)或者传播(transmitted)
  3. 光速无穷大*(光以无限快的速度沿直线传播)
  1. 在某些极其特殊的光照模型(需要光程差)中不适用，不过实时渲染中暂时没有使用这些光照模型的可能

图形学使用的几何光学定理

       光入射到物体表面时，同时发生反射和折射。

菲涅尔

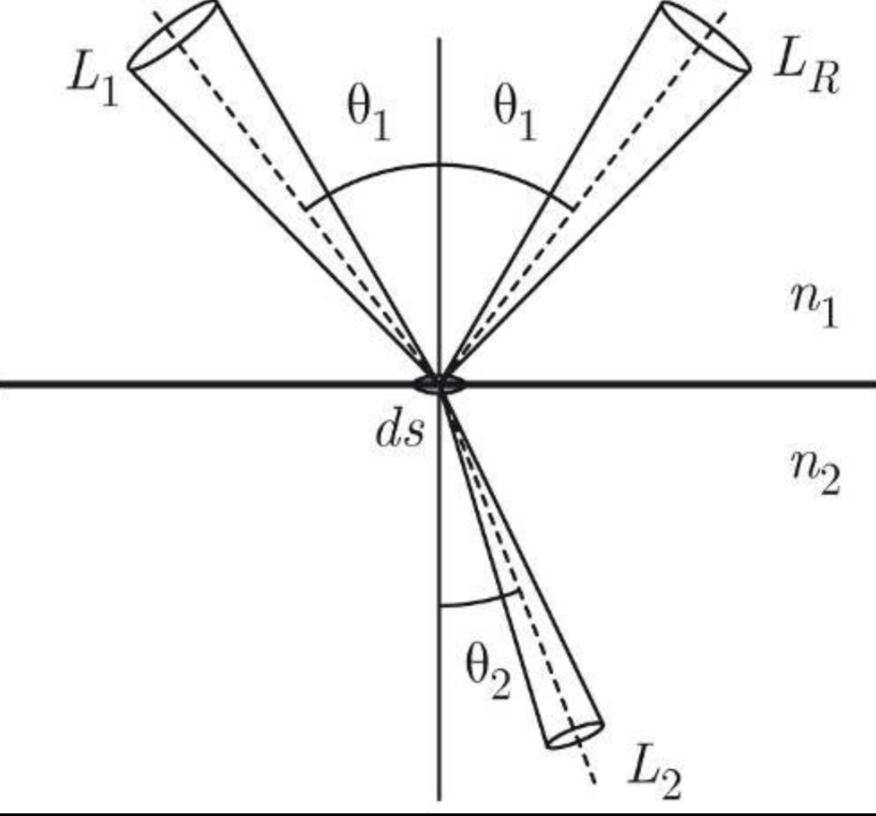
1. 反射定理

       光射到一个界面上时，其入射光线与反射光线成相同角度

\[\theta_1 = \theta_1\]

2. 折射定理

  1. 折射光线位于入射光线和界面法线所决定的平面内；
  2. 折射线和入射线分别在法线的两侧；
  3. 入射角 $\theta_1$ 的正弦和折射角 $\theta_2$ 的正弦的比值，对折射率一定的两种媒质来说是一个常数。
\[n_1 sin \theta_1 = n_2 sin \theta_2\]

3. 菲涅尔定理

       在计算机图形学中，人眼看到的是物体表面反射的光，因此我们要求出物体表面反射部分光线的能量。

\[L_2 = (1 - R_F(\theta_1))\frac{n_2^2}{n_1^2}L_1\]

       该公式在计算时依旧过于复杂，所以实际计算时一般使用菲涅尔反射能量公式的Schlick近似公式：

\[R_F(\theta_i) \approx R_F(0^o) + (1 - R_F(0^o))(1 - \overline{cos}\theta_i)^5\]

       反射率随入射角变化曲线：

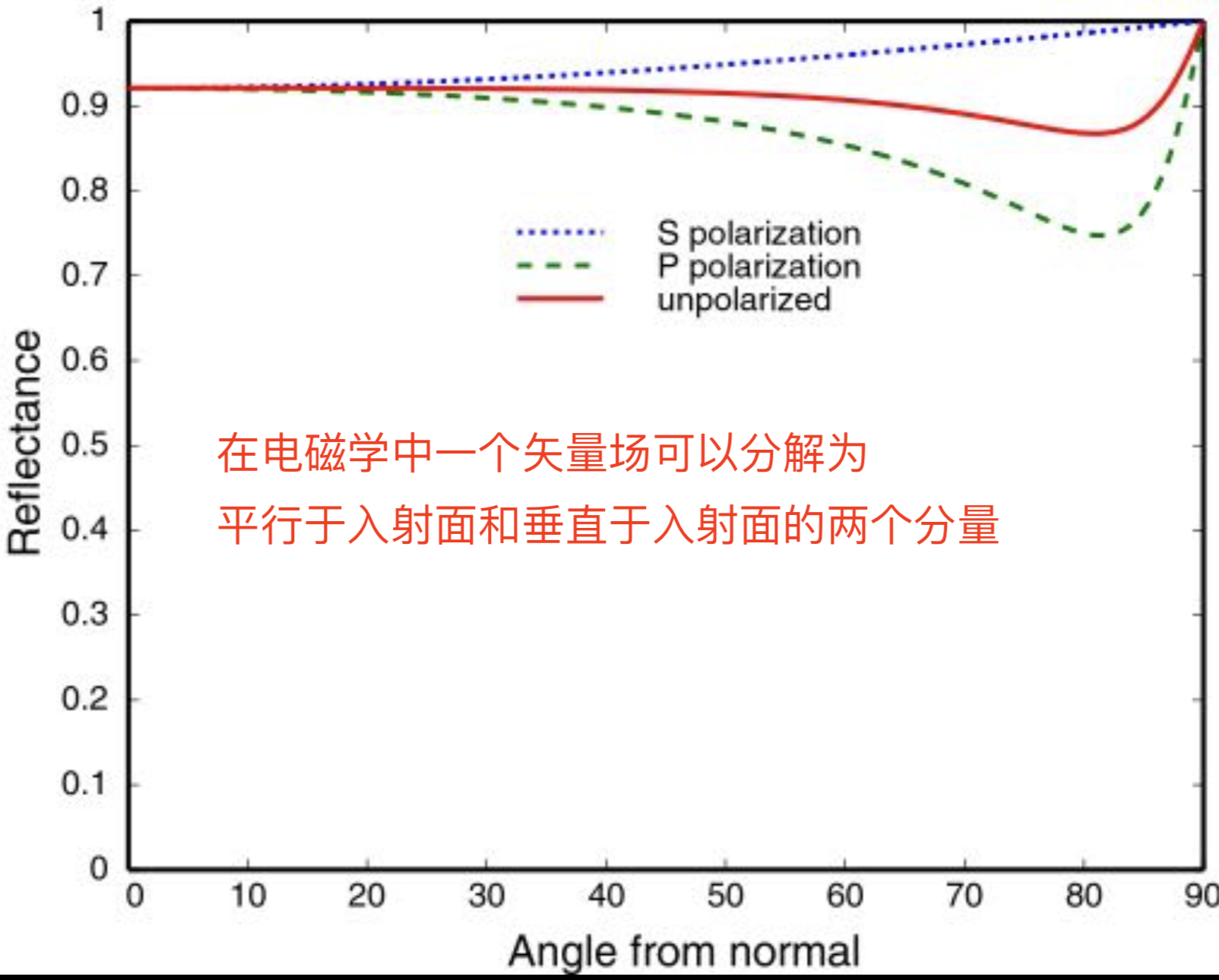
金属： 菲涅尔曲线-金属

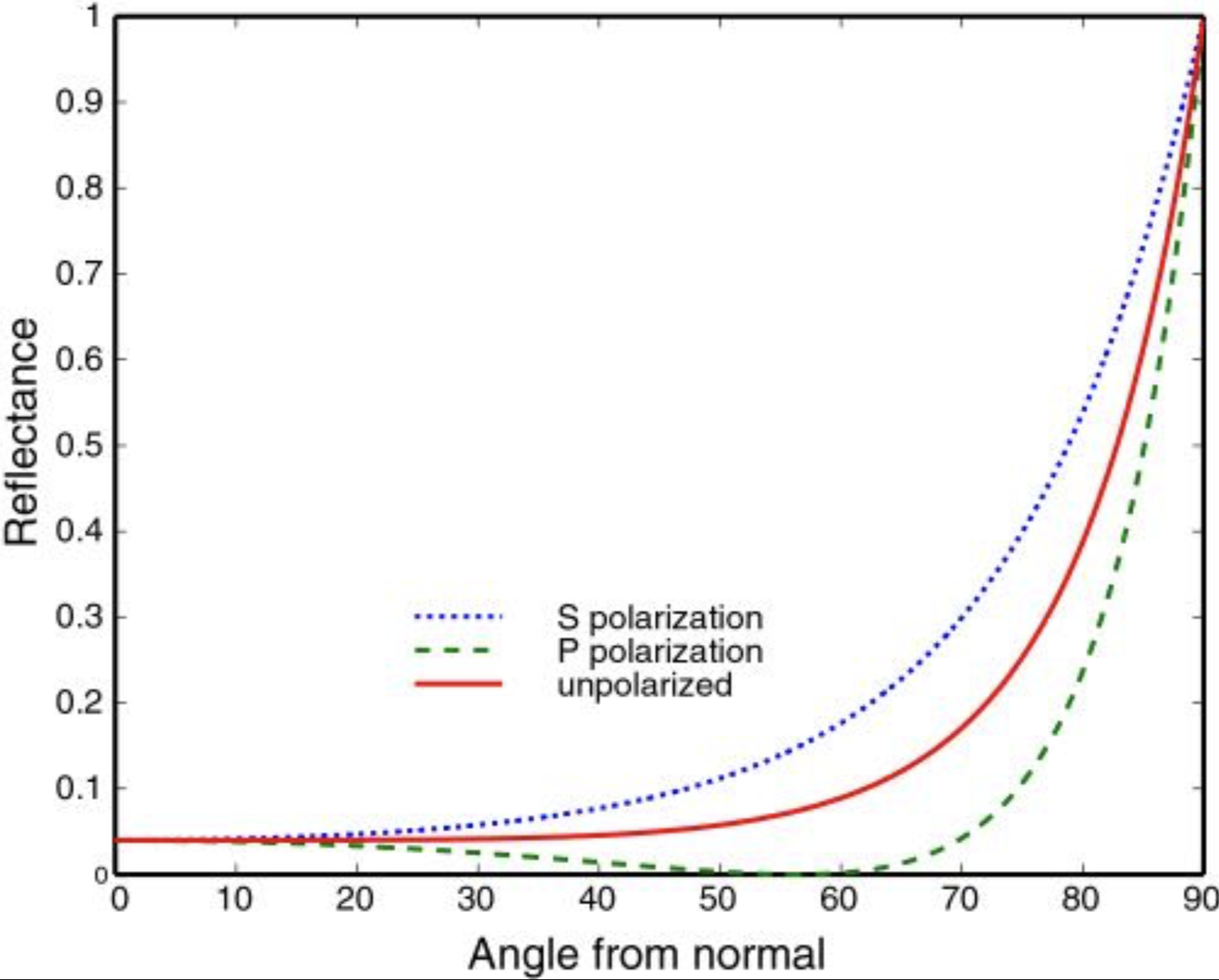
非金属： 菲涅尔曲线-非金属

现象

       在接近平行物体表面观察的情况下，非金属平整表面也有很明显的镜面效果。

由光学定理推导渲染方程

       在这里推导GGX BRDF。

1. 图形学中几何光学模型的限制

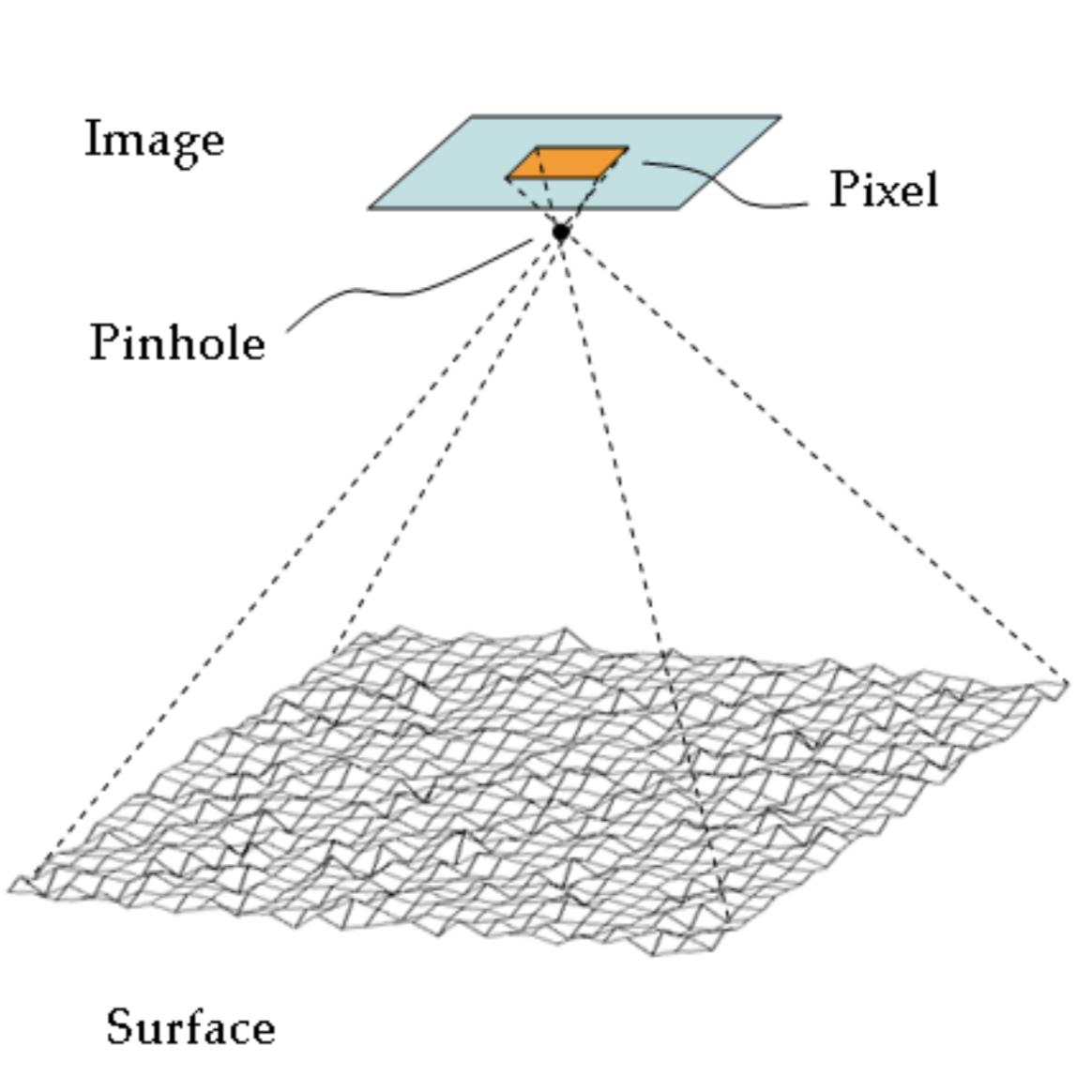
物体表面实际情况

       目前为止的理论要求我们所处理的表面是绝对光滑的，但只有相当于微观原子尺寸上，表面才可能绝对光滑，在实际物体表面物体是有微小的无规则起伏的。

2. 微面元理论

       核心思想：使用一个统计分布函数来描述微观尺寸

       假设我们能够处理微观尺寸，则来自同一个方向的光照会被反射至多个方向。那么只要能够模拟这个行为，就能在像素尺寸模拟微观结构的光学行为。所以可以定义一个法线分布函数，以代替单个像素的法线值。

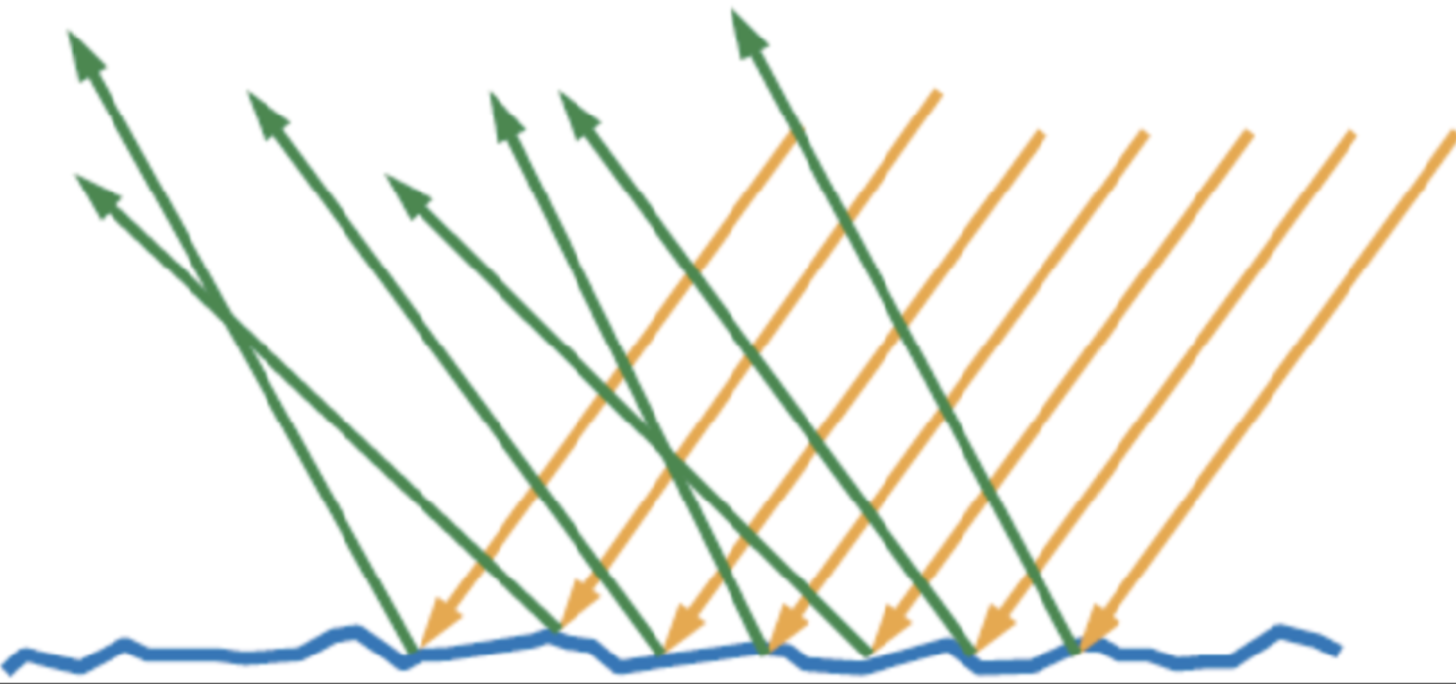
微面元理论

3. 法线分布函数D

       法线分布函数表示微面元发现方向的统计分布。给定一个入射方向，一个微面元有多大概率朝向半向量方向。

半向量

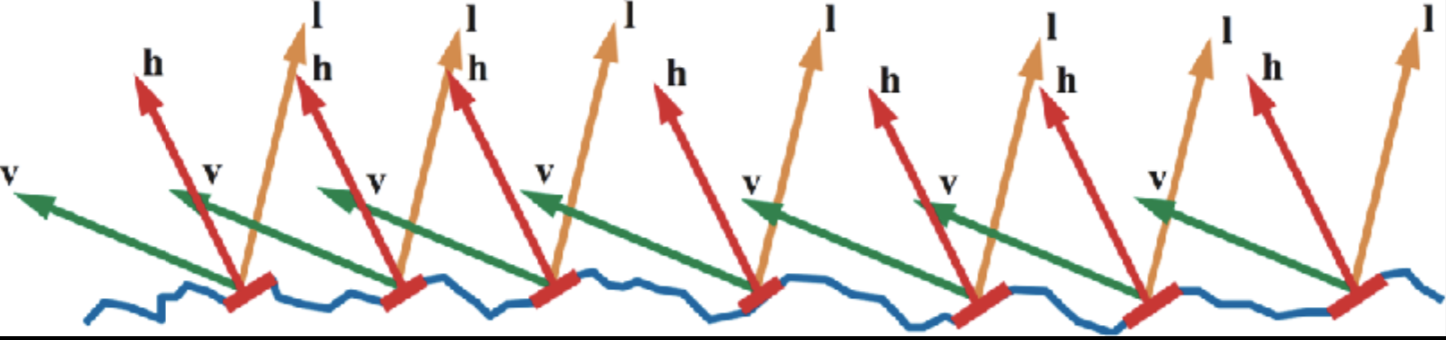
       法线分布函数有各向同性、各向异性之分。

       对于GGX(二维函数，园对称)，只需要表面的

\[D(h) = \frac{\alpha^2}{\pi \lgroup (n \cdot h)^2(\alpha ^ 2 - 1)+1 \rgroup ^2}\]

       法线分布函数虽然模拟了表面的凹凸的情况，但是缺忽略了一个问题，那就是微面元上光线被凹凸遮挡的问题。

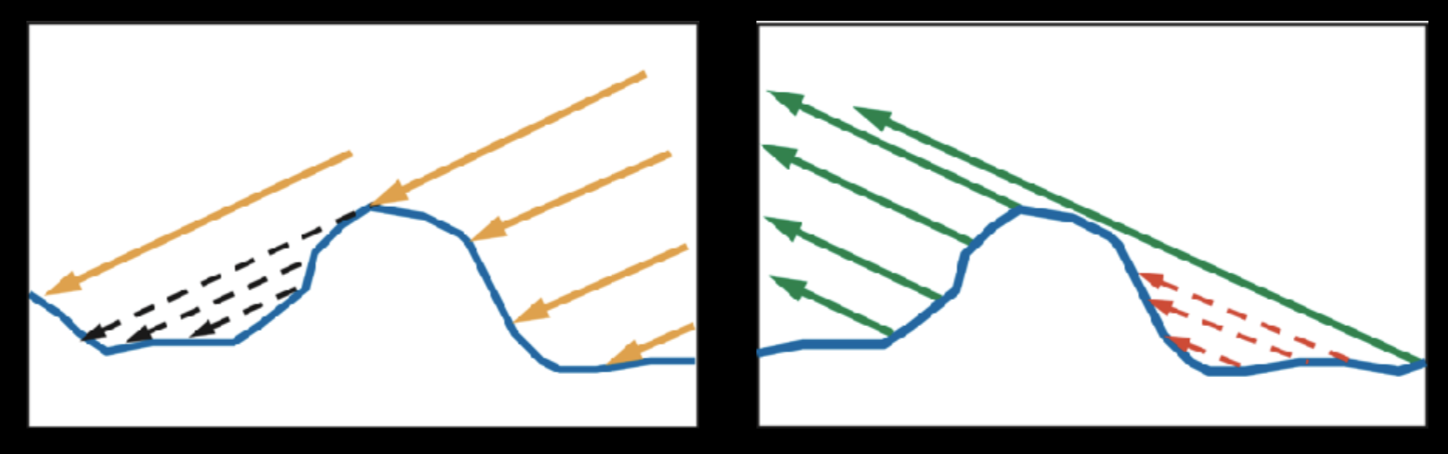
微面元上光线被凹凸遮挡

       为了解决这个问题，引入一个阴影补偿函数G，来模拟表面凹凸遮挡阴影的情况。

4. 双向阴影遮挡函数G

       NDF假设所以微面元位于同一平面，不考虑实际几何结构导致的遮挡。它描述的是那些具有半向量法线的微面元中，有多少比例是同时被入射方向和反射方向看到的(或者说没有被阻挡的)，一般使用史密斯阴影函数。

\[k = \frac{(\alpha + 1)^2}{8}\] \[G_1(v) = \frac{n \cdot v}{(n \cdot v)(1 - k) + k}\] \[G(l, v, h) = G_1(l)G_1(v)\]

用来补偿的阴影遮挡函数G是一个纯粹的经验模型，没有任何光学理论的支撑。函数 $G_1$ 表示光没有被凹凸表面遮挡的概率。将入射光和反射光概率相乘就是整个光路光线不被遮挡的概率。所谓双向，就是入射光和反射光两个方向

       现在我们有了物体表面能量的表示方法。由于我们只关心反射能量，所以上述公式还要再乘以菲涅尔公式，就是物体表面的反射能量。

5. 双向分布函数BRDF

\[f(l, v) = \frac{D(h)F(v, h)G(l, v, h)}{4(n \cdot l)(n \cdot v)}\]

6. BRDF的物理性质

       解释一下BRDF的能量守恒。BRDF能量遵循如下公式。

\[f_r(\omega_i, \omega_r) = \frac{\mathrm{d} L_r(\omega_r)}{\mathrm{d} E_i(\omega_i)} = \frac{\mathrm{d} L_r(\omega_r)}{L_i(\omega_i)cos\theta_i \mathrm{d} \omega_i}\] \[f_r(\omega_i, \omega_r) = f_i(\omega_r, \omega_i)\] \[\int_\Omega f_r(\omega_i, \omega_r) cos\theta_i \mathrm{d} \omega_i \leqslant 1, \forall \omega_r\]

       BRDF并不一定遵循能量守恒，只能保证反射出的总能量不大于入射的能量。就是说，BRDF模型发射光相比真实的物理情况可能要暗一些。

7. 其他常见的BRDF模型

Blinn-Phong，简单快速，各向同性，表达能力有限：

\[D(h) = \frac{\alpha + 2}{2 \pi}cos^{\alpha}(\delta)\] \[G(l,v,h) = (n \cdot l)(n \cdot v)\]

Cook-Torrance，复杂一些，各向同性，可以较好地表达真实材质：

\[D(h) = \frac{1}{\pi \beta^2 cos^4(\delta)}e^{-\frac{tan^2(\delta)}{\beta^2}}\] \[G(l,v,h) = min \{1, \frac{2(n \cdot h)(n \cdot v)}{v \cdot h}, \frac{2(n \cdot h)(n \cdot l)}{v \cdot h} \}\]

Ward，复杂一些，支持各向异性：

\[D(h) = \frac{1}{\pi \alpha^2}e^{-\frac{tan^2(\delta)}{\alpha^2}}\] \[G(l,v,h) = \sqrt{(n \cdot l)(n \cdot v)}\]